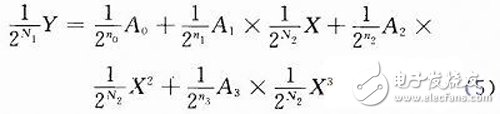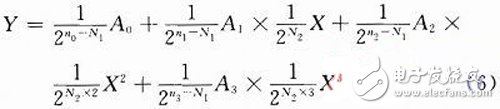Traditional DSPs are based on CPU architecture and are processors based on specific instruction systems, but as the operating clock gets closer to the limits acceptable to electronic devices, the processing power of such DSPs is close to its limits; With the development of EDA technology, especially the maturity and application of FPGA and CPLD devices, parallel computing can be realized by directly designing the circuit, so that the efficiency of the operation is improved in essence, and it can realize very complicated in real time. Computing, so FPGA-based computing devices are on the agenda and are receiving more and more attention. An algorithm that is easy to implement with circuitry and is versatile, helping engineers to easily and efficiently design an operator that can work on an FPGA. The preliminary FPGA design is to describe the logic function of the device in hardware description language. A good design must consider the characteristics of the digital circuit. The CPU is a typical digital circuit, because it can only do addition operations, so it is necessary to convert various operations into addition by a program. The traditional "numerical analysis" is formed on the basis of this kind of programming. It is not only complicated but also inefficient, and can not realize real real-time operation. In addition to the addition operation, the FPGA itself can do the subtraction of unsigned numbers. Multiplication is also very convenient. At present, the integrated development software introduced by the two major FPGA manufacturers has integrated IP cores for addition, subtraction and multiplication, and the operation efficiency is very high. For an unsigned number operation, generally only one clock or even a combination of clocks is not required. Logic circuits, as well as a detailed description of these operators in the literature. However, the direct division method is different. Although there are division IP cores, it requires many clocks and takes up a lot of logic resources, which is inconvenient for design and application. Another disadvantage of circuit operations is that it is cumbersome to represent signed numbers and fractions, and to do operations between signed fractions. Therefore, when designing DSP, I always hope to find a way to avoid as much as possible. The role of the operator is to perform various operations on the data. This process can be represented by a function: y = f(x). Any function that is continuous around zero can be expanded to the McLaughlin series: The high-order derivative terms of most commonly used functions are small or zero, so the finite term can be taken within the range allowed by precision, that is, a polynomial is used for approximation. The characteristics of polynomial operations are described in detail in the literature. It is very convenient to implement polynomial operations with FPGAs and handle many complex functions. This article discusses an operator that can implement polynomial (2) operations using FPGAs or CPLDs. For a simple polynomial, it can be a combinational logic circuit, which does not require a clock, so the operation efficiency is high. Many of these operations can be done simply and efficiently. The arithmetic circuits between various unsigned integers are outlined in the literature. Although the calculation of the number of symbols represented by the inverse code can also be performed, it is not preferred. Because it is necessary to do four mixed operations; the inverse code is easy to add and subtract, but it is not easy to do multiplication and division. With non-inverted coded bit data, the sign bit is calculated separately, and the rest of the data is unsigned. The entire calculation structure is the simplest. In addition, even the division of unsigned numbers is complicated, but considering that there is a special division operation, it is equivalent to dividing the binary digit by the last digit. Therefore, you can avoid dividing by a number other than 2 in order to simplify the calculation. It can also be considered as an integer calculation in an operation. This is done by using unsigned fixed-point numbers, and with independent sign bits indicating positive and negative, you can perform complex operations with a simple unsigned operator. Equation (4) is a 3rd degree polynomial. Let it introduce the design method as an example: First, all the numbers in equation (4) are represented by one sign bit plus an unsigned binary form. Using N1, N2 to represent the number of decimal places contained in y and x, you can write equation (4) as: In the formula: X, Y is x, y removes the integer after the decimal point (Note: here is the same as equation (3) just remove the decimal point, not remove the decimal place). A0, A1, A2, and A3 are also the same as the constants of the system; n0, n1, n2, and n3 are the decimal places in the binary form of a0, a1, a2, and a3, respectively. The equation (5) can be further transformed as: It is not difficult to find that equation (6) is very easy to implement. The calculation of each sign bit is performed first, and then only the unsigned integer data is calculated; and the division is all divided by a multiple of 2. The final item is added and subtracted according to the sign bit to obtain the output Y, which is a fixed-point number with a sign of N1 decimal places. General Purpose Rectifier Bridge
A bridge rectifier provides full-wave rectification from a two-wire AC input, resulting in lower cost and weight as compared to a rectifier with a 3-wire input from a transformer with a center-tapped secondary winding.
Our company mainly produces diodes, which are sold overseas.Has a stable source of customers, product quality by customers trust.
Our products are the ideal choice of printed circuit board, we have reliable low-cost construction technology, product price cost-effective, welcome to come to consult.
Bridge Rectifiers,GBU General Purpose Rectifier Bridge,General purpose Rectifier diodes,General Purpose Bridge Rectifiers Changzhou Changyuan Electronic Co., Ltd. , https://www.cydiode.com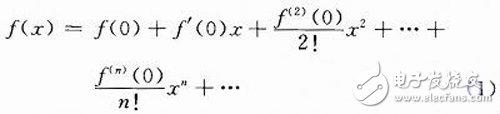
y=a0+a1&TImes;x+a2&TImes;x2+...+an&TImes;xn (2)
Indicates that decimals are required in the calculation. Binary fixed-point fractions are introduced in the literature. For example, a 2-bit binary fraction that requires a reserved number can be expressed as: (b3b2b1.a1 a2): 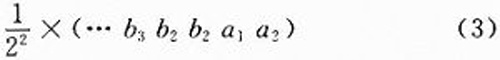
y=a0+a1&TImes;x+a2×x2+a3×x3 (4)