In 1959, Widrow and Hoff proposed the least mean square algorithm (LMS algorithm) when studying the pattern recognition of adaptive linear elements. The LMS algorithm is based on Wiener filtering and is then developed by means of the steepest descent algorithm. The Wiener solution solved by Wiener filtering must be determined by knowing the a priori statistical information of the input signal and the desired signal, and recalculating the autocorrelation matrix of the input signal. Therefore, this Wiener solution is only an optimal solution in theory. Therefore, with the help of the steepest descent algorithm, the Wiener solution is approximated in a recursive manner, thereby avoiding the matrix inversion operation, but the a priori information of the signal is still needed, and then the square of the instantaneous error is used instead of the mean square error. The result is the LMS algorithm. Because the LMS algorithm has the characteristics of low computational complexity, good convergence in the environment where the signal is a stationary signal, its expected value converges unbiasedly to the Wiener solution and the stability of the algorithm with limited precision, the LMS algorithm becomes self-sufficient. The best and most widely used algorithm in adaptive algorithms. The following figure is a vector signal flow diagram of the implementation algorithm: Figure 1 LMS algorithm vector signal flow chart As can be seen from Figure 1, the LMS algorithm mainly consists of two processes: filtering processing and adaptive adjustment. In general, the specific process of the LMS algorithm is: (1) Determine parameters: global step size parameter β and the number of taps of the filter (also called filter order) (2) Initialization of the initial value of the filter (3) Algorithm operation process: Filtered output: y(n)=wT(n)x(n) Error signal: e(n)=d(n)-y(n) Weight coefficient update: w(n+1)=w(n)+βe(n)x(n) To a large extent, what adaptive algorithm is chosen determines whether the adaptive filter has good performance. Therefore, performance analysis of the most widely used algorithmic algorithms is particularly important. The main performance indicators of the algorithm in the stationary environment are convergence, convergence speed, steady state error and computational complexity. 1. Convergence Convergence means that when the number of iterations tends to infinity, the filter weight vector will reach the optimal value or be in a neighborhood close to it, or it can be said that the filter weight vector eventually approaches when a certain convergence condition is satisfied. At the optimal value. 2, convergence speed The convergence speed refers to the degree to which the filter weight vector converges from its initial initial value to its optimal solution. It is an important indicator to judge the performance of the LMS algorithm. 3, steady state error The steady-state error refers to the distance between the filter coefficient and the optimal solution when the algorithm enters the steady state. It is also an important indicator to measure the performance of the LMS algorithm. 4, the computational complexity The computational complexity refers to the amount of computation required to update the filter weight coefficients once. The computational complexity of the LMS algorithm is still very low, which is also a major feature of it. 1. Quantization error LMS algorithm In applications such as echo cancellation and channel equalization that require adaptive filters to operate at high speeds, it is important to reduce computational complexity. The computational complexity of the LMS algorithm mainly comes from the multiplication operation in the data update and the calculation of the adaptive filter output. The quantization error algorithm is a method to reduce the computational complexity. The basic idea is to quantify the error signal. Common symbolic error LMS algorithm and symbol data LMS algorithm. 2. De-correlated LMS algorithm In the LMS algorithm, there is an independence assumption that the inputs u(1), u(2), ..., u(n-1) of the transversal filter are statistical sequences that are statistically independent of each other. When the statistically independent conditions are not met between them, the performance of the basic LMS algorithm will decrease, especially the convergence speed will be slower. To solve this problem, propose to understand the relevant algorithms. Research shows that the decorrelation can effectively accelerate the convergence speed of the LMS algorithm. The decorrelated LMS algorithm is further divided into a time domain decorrelation LMS algorithm and a transform domain decorrelation LMS algorithm. 3. Parallel delay LMS algorithm In the implementation structure of the adaptive algorithm, there is a kind of pulsation structure for VLSI, which has attracted much attention due to its high parallelism and pipeline characteristics. When mapping algorithms directly to pulsating structures, there are serious computational bottlenecks in weight update and error calculation. The algorithm solves the computational bottleneck problem of the algorithm to the structure, but when the filter order is long, the convergence performance of the algorithm will be worse, which is because its own delay affects its convergence performance. It can be said that the delay algorithm is at the expense of the convergence performance of the algorithm. 4. Adaptive lattice LMS algorithm The LMS filter belongs to the transverse adaptive filter and assumes that the order is fixed. However, in practical applications, the optimal order of the transversal filter is often unknown, and it is necessary to determine the optimal order by comparing filters of different orders. . When changing the order of the transversal filter, the LMS algorithm must be re-run, which is obviously inconvenient and time consuming. The lattice filter solves this problem. The lattice filter has a conjugated symmetrical structure, and the forward reflection coefficient is a conjugate of the retroreflection coefficient. The design criterion is the same as the LMS algorithm to minimize the mean square error. 5. Newton-LMS algorithm The Newton-LMS algorithm is an algorithm that estimates the second-order statistics of environmental signals. The purpose is to solve the problem that the algorithm converges slowly when the input signal correlation is high. In general, the Newton algorithm can converge quickly, but the calculation of R-1 requires a large amount of computation, and there is a problem of numerical instability. Copper Tube Terminals Without Checking Hole Our company specializes in the production and sales of all kinds of terminals, copper terminals, nose wire ears, cold pressed terminals, copper joints, but also according to customer requirements for customization and production, our raw materials are produced and sold by ourselves, we have their own raw materials processing plant, high purity T2 copper, quality and quantity, come to me to order it! Copper Tube Terminals Without Checking Hole,Cable Lugs Insulating Crimp Terminal,Cable Connector Tinned Copper Ring Terminal,Tubular Cable Lugs Crimp Terminal Taixing Longyi Terminals Co.,Ltd. , https://www.longyiterminals.com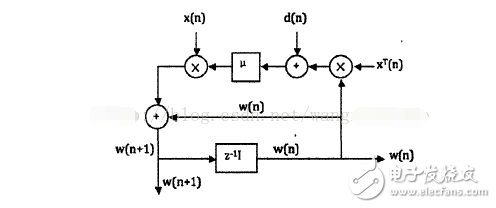
Basic idea and principle of lms algorithm
I. Overview of the Least Mean Square Algorithm (LMS)