The weight of the tree: the number of each tree node. Path: The branch that passes between two nodes. Path length: The number of branches on a path. Node weighted path length: The weight of the node * The path length of the node. Tree weight path length: The sum of the full path lengths of all leaf nodes. Tree weight path length: The sum of the full path lengths of all leaf nodes. a, path and path length If there is a sequence of nodes k1, k2, ..., kj in a tree, so that ki is the parent of ki+1 (1 "=i"j), then the sequence of nodes is called from k1 to kj path. The number of branches passing from k1 to kj is called the path length between the two points, which is equal to the number of nodes on the path minus 1. b, the weight of the node and the length of the weighted path In many applications, the nodes in the tree are often given a real number with some meaning. We call this real number the weight of the node (as the blue number in the tree below indicates the weight of the node) The weighted path length of a node is defined as the product of the path length from the root node to the node and the weight on the node. c, the length of the weighted path of the tree The weighted path length of a tree is defined as the sum of the weighted path lengths of all leaf nodes in the tree. The formula is: Where n is the number of leaf nodes, and wi and li represent the weight of the leaf node ki and the path length between the root node and ki, respectively. The weighted path length of the tree in the following image is WPL = 9 x 2 + 12 x 2 + 15 x 2 + 6 x 3 + 3 x 4 + 5 x 4 = 122 d, Huffman tree The Huffman tree is also known as the optimal binary tree. It is a binary tree with the smallest WPL of the weighted path length among all the binary trees composed of n weighted leaf nodes. The following picture shows a Huffman tree diagram. 72V Battery Pack ,Lithium Ion Battery Pack,Lithium Battery Pack,Battery Power Pack Zhejiang Casnovo Materials Co., Ltd. , https://www.casnovonewenergy.com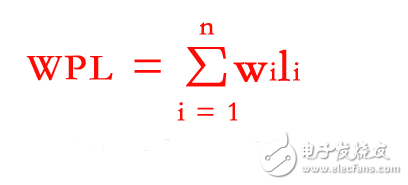
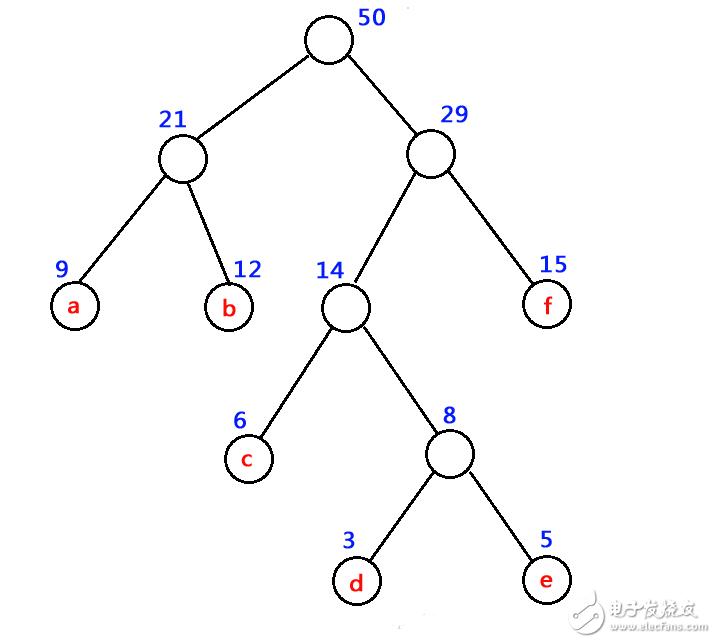
Basic concept and construction of Huffman tree
Noun meaning in the Huffman tree