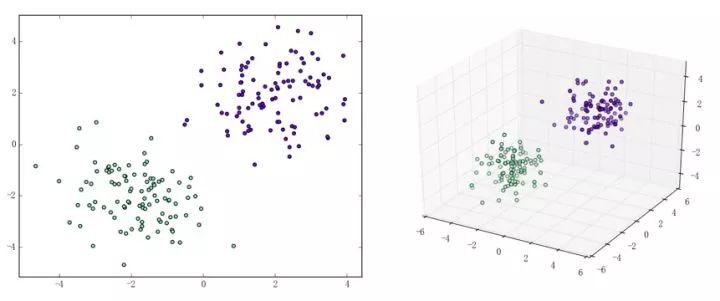
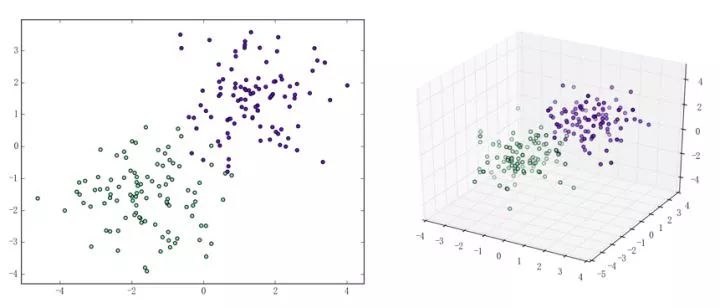
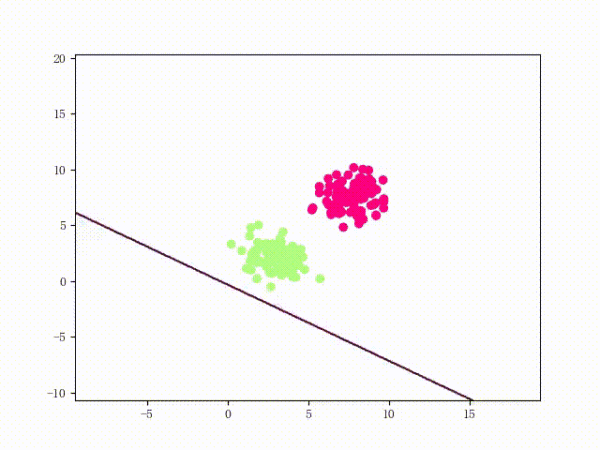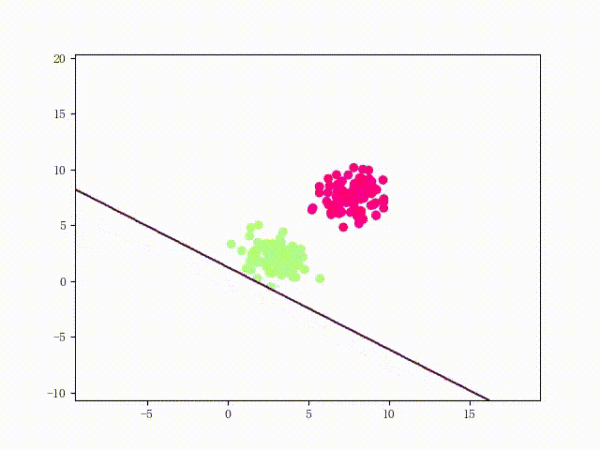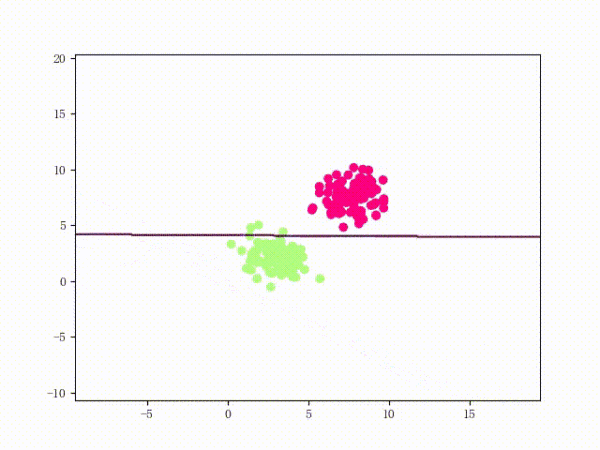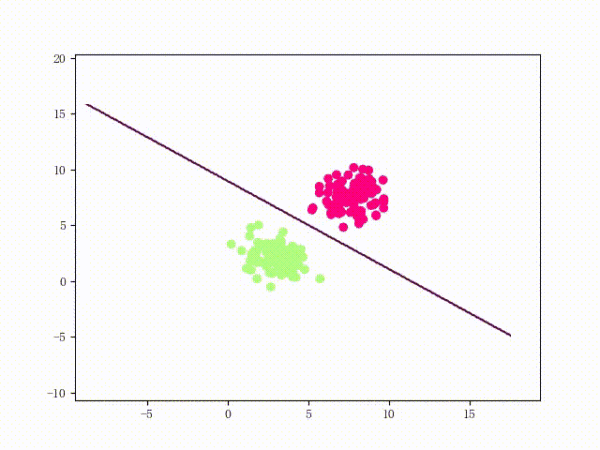
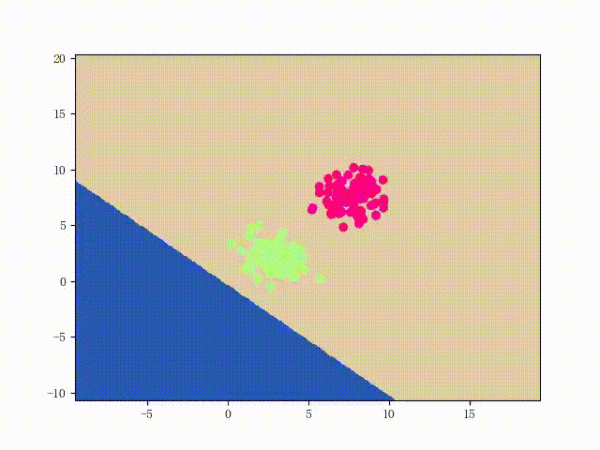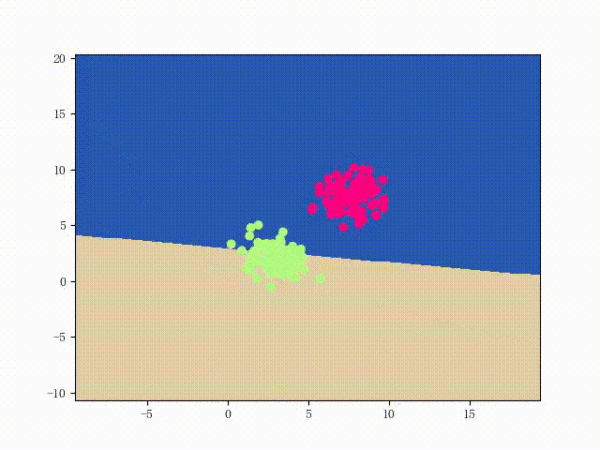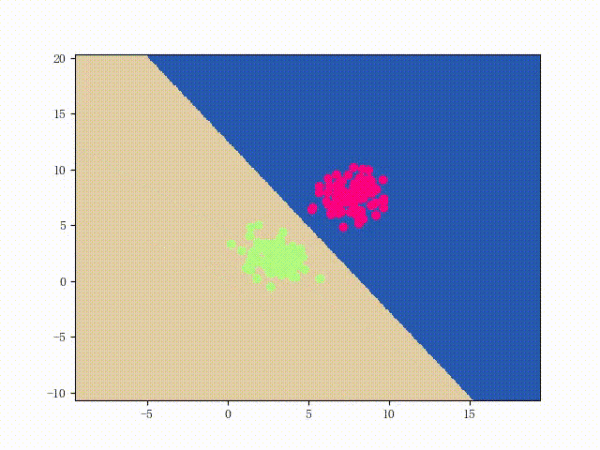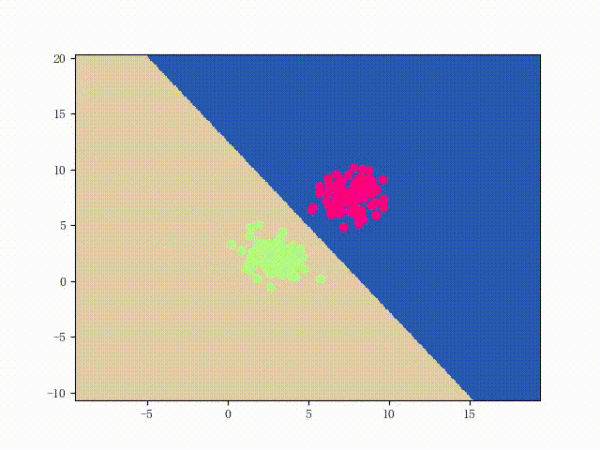
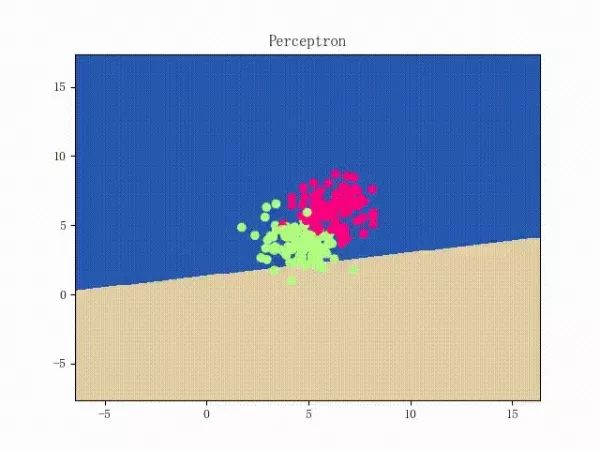
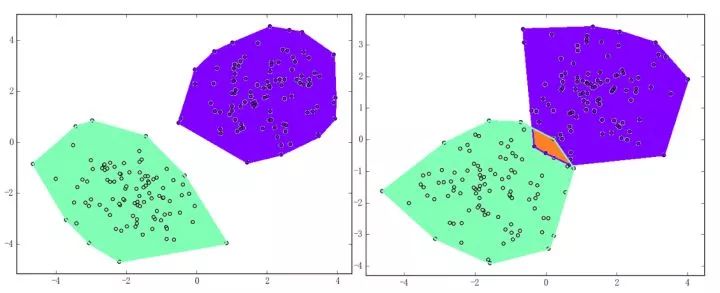
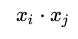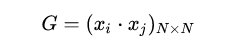The perceptron is a fairly simple model, but it can also evolve into a support vector machine (by simply modifying the loss function), but it can also develop into a neural network (by simply stacking), so it also has a certain position. For convenience, we discuss the two-class problem in a unified manner and refer to the two categories of samples as positive and negative samples respectively. What does perception function do? The perceptual function (and certainly some) separates the linearly separable data sets. What is linearly separable? In the two-dimensional plane, linear separability means that the positive and negative samples can be separated by a single line. In three-dimensional space, linear separability means that one plane can be used to separate positive and negative samples. You can intuitively feel the concepts of linear separability (above) and linear separability (below) using two graphs: So how does a perceptron separate linearly separable data sets? The following two motion pictures may give viewers some intuitive feelings: It seems very quick, but we can rest assured that as long as the data set is linearly separable, the perceptron must be able to “sweep†to a place where the data set can be separated (the proof will be attached at the end). In turn, if the data set is linearly inseparable, how will the perceptron behave? Believe that the clever audience lords have already guessed: it will always "dust and run" (the last stop is because of the iterative limit) (and then it looks like the move is too large to cause a residual image ... but the effect is not bad so Will just look at it (σ'ω')σ): Class Perceptron: def __init__(self): self._w = self._b = None def fit(self, x, y, lr=0.01, epoch=1000): # convert input x, y to numpy array x, y = np.asarray(x, np.float32), np.asarray(y, np.float32) self._w = np.zeros(x.shape[1]) self._b = 0. The above fit function has a lr and an epoch, which represent the learning rate and the upper limit of iteration in the gradient descent method respectively. (Ps from the following derivation, we can prove that for the perceptron model, in fact, the learning rate does not affect the convergence. Sex [but may affect the speed of convergence]) Gradient descent we are more familiar with. In simple terms, the gradient descent method consists of the following two steps: Find the gradient of the loss function (Derivation) Gradient is the direction in which the value of the function grows fastest. We want to minimize the loss function. We want to reduce the value of the function the fastest. Move the parameter in the opposite direction of the gradient. (This is why gradient descent is sometimes called the steepest descent. Gradient descent is commonly used in neural networks, convolutional neural networks, and other networks. If you are interested, see this article (https:/ /zhuanlan.zhihu.com/p/24540037)) What is the loss function for the perceptron model? Notice that the perceptron corresponding to our hyperplane is For _ in range(epoch): #Calculate w x +b y_pred = x.dot(self._w) + self._b # Select the sample idx = np.argmax that maximizes the loss function (np.maximum(0, -y_pred * y)) # If the sample is correctly classified, end the training if y[idx] * y_pred[idx] > 0: break # Otherwise, let the parameter go one step in the negative gradient delta = lr * y[idx ] self._w += delta * x[idx] self._b += delta So how does a perceptron separate linearly separable data sets? The following two motion pictures may give viewers some intuitive feelings: At this point, the perceptron model is roughly finished, and the rest is pure mathematics, which is generally not regarded as problematic. Related mathematical theory That is, the number of training steps is upper bound, which means convergence. In addition, the learning rate is not included, which means that the learning rate does not affect the convergence of the perceptron model. Finally, a very important concept is briefly introduced: Lagrange Duality. The perceptron algorithms we introduced in the first three subsections can actually be called the "perceptual machine's original algorithm." With Lagrangian duality, we can get the dual form of perceptron algorithms. Given that the original form of Lagrange's duality is too pure mathematics, I intend to introduce it in terms of concrete algorithms, without intending to describe its original form. The interested audience can see here (https://en.wikipedia.com). Org/wiki/Duality_(optimization)) In the constrained optimization problem, we often use it to convert the original problem into a better solution to the dual problem in order to facilitate the solution. For specific problems, the duality of the original algorithm often has some commonalities. For example, for perceptrons and support vector machines to be described later, their dual algorithms will represent the parameters of the model as some linear combination of sample points and transform the problem into solving the coefficients in the linear combination. Although the original form of the Perceptron algorithm has been very simple, by converting it to the dual form, we can more clearly feel the process of transformation, which helps to understand and memorize the more complex SVMs described later. Dual form Considering the core steps of the original algorithm are: This is the dual form of the perceptron model. It should be pointed out that in the dual form, the x in the sample point only takes the inner product ( Note that the dual-form training process often uses a large number of inner products between sample points. We usually calculate the inner product between two sample points in advance and store it in a matrix; this matrix is ​​famous. The Gram matrix, its mathematical definition is: So if you want to use the corresponding inner product in the training process, you only need to extract from the Gram matrix, which can greatly improve efficiency in most cases. The reason why portable Solar Panels are most popular is that you can use them on camping. these small solar panels will give you the electricity to run your appliances during camping in remote areas. it is the best way to use it. due to their portability, they are easy to carry on and easy to set up. portable solar panels for camping, solar powered powerbank, portable solar power station, solar camping power, portable solar power Jiangxi Huayang New Energy Co.,Ltd , https://www.huayangenergy.com